Study 1 Question 3:

How consistent is the average rating for each sex?

As mentioned in Question 2, averaging can be problematic because it does not show the variance of the answers. This question examines the variance of participants' ratings to determine how appropriate the averages are for representing the rating, and explores how or if the two sexes varied in their ratings of gendered statements.

Studying the results of each of the 48 statements would be time consuming and the results may become repetitive. So, I examined this question by first choosing a subset of statements to analyze. Figure 5 shows the selected statements' average answers by sex. I chose statements that either had similar averages for both sexes or different averages by sex. It is possible that variance similarities between the sexes may be determined by the average similarities. Perhaps statements where the average of the two sexes were similar, the variance in answer that the two sexes may have would also be similar. Or, perhaps when the averages were different the similarities in variances may be more similar than when the averages are similar. I explore this by choosing to analyze two statements that had similar averages and three statements that had different averages. Statements 3 and 19 were chosen because the averages for both sexes were similar and statements 6, 19, and 28 were chosen because they had different averages. Table 1 lists the questions I chose and why.

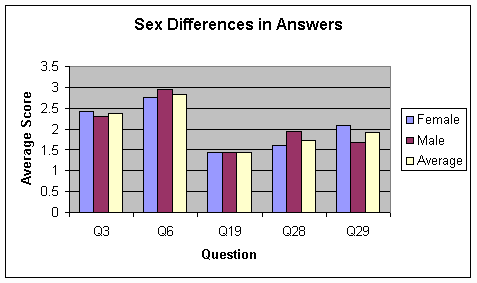
Figure 5: Average Answers by Sex to Select Statements

Table 1: Selected Statements for Variance Comparisons with Similar or Different Averages

After determining which questions to study, I found the number of answers each gender had for these questions (Figures 6A and 6B). This illustrates the variance by displaying the number of times females or males rated a certain statement feminine, masculine, or neutral. It is interesting to see how some statements were almost completely rated as masculine and others showed the ratings were dispersed more evenly. For instance, most males rated statement 6 as masculine, only one did not. One the other hand, for statement 29 the answers were more diverse.

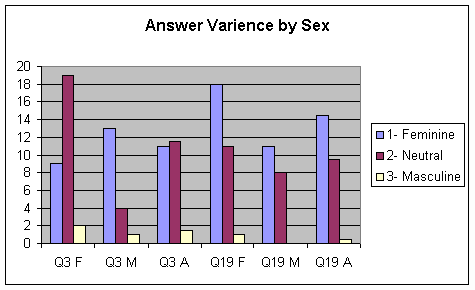
Figure 6A: Number of Answers by Sex with Overall Average for "Similar" Statements

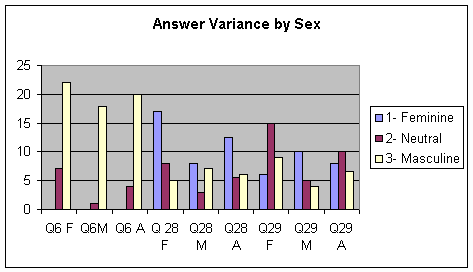
Figure 6B: Number of Answers by Sex with Overall Average for "Different" Statements

Charting the answers shows how the sexes did differ visually, but does not give numbers of the actual variance. So, I found the standard deviation of each statement by sex and then calculated the overall average standard deviation by sex. Table 3 shows the results and Figure 7 a visual representation of the results. The standard deviation shows there was some ratings variance by sex. For instance, on Question 6, the males' answers deviated much more greatly than the females'. However, the average of the deviations (listed in Table 3) shows there was an insignificant amount between the sexes for these five questions.

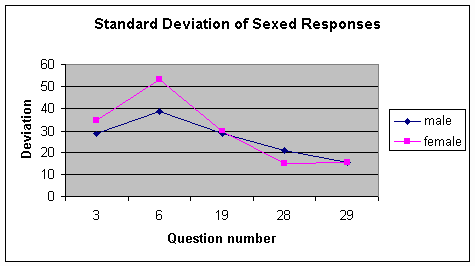
Figure 7: Standard Deviation of Sexed Responses

The similar deviation suggests that although for some statements the females and males may have had greater variance in ratings, overall the variance was similar for the two sexes. This is variance similarity is important because it suggests that the averaging I used in Questions 1 and 2 to analyze results is less problematic. Since both sexes had similar variance, the averages offer a clearer, more appropriate picture of the results. The similar variance suggests that the average represents each sex equally and whatever variance it might hide for one sex is similar to the hidden variance for the other sex.

Table 3: Standard Deviation for Sex by Question

Study One:

Procedure | Analysis and Results: Question 1, Question 2, Question 3, | Discussion